La beauté modulaire des tables de multiplication

Détails: Mis à jour : 12 avril 2022

Question : faut-il être fou pour parler d'arithmétique modulaire à un collégien ?
Réponse : non ! On l'utilise même tous les jours en regardant l'heure...

L'idée de base de l'arithmétique modulaire est de travailler non sur les nombres eux-mêmes, mais sur les restes de leur division par quelque chose.
Par exemple, s’il est 16h52 et que j’attends 15 minutes, il sera 17h07, autrement dit 52+15=7 dans l’arithmétique (des minutes) de l’horloge.

Ce que nous en écrivons, en mathématiques :

52 + 15 \(\equiv\) 7 (mod. 60)

et que nous lisons :

« 52 plus 15 est congru à 7 modulo 60 ».

Pourquoi congru ? En latin, congruens signifie « qui s'accorde ».
Pourquoi modulo ? Il s’agit de l'ablatif du nom latin modulus, qui signifie « mesure ».

Le symbole \(\equiv\) est l’œuvre du prince des mathématiciens, Carl Friedrich Gauss, qui publie en 1801 l’ouvrage Disquisitiones arithmeticae, et donne ainsi une naissance rigoureuse à l’arithmétique modulaire, qui révolutionnera la théorie algébrique des nombres mais aussi notre quotidien, puisque l'arithmétique de base des ordinateurs travaille sur des « nombres » de taille fixe, et est par conséquent une arithmétique modulaire.

Pour lire la sublime biographie de Gauss, c'est dans un autre article : cliquer ici.

Vous comprenez maintenant, je l’espère, les congruences suivantes :

5 \(\equiv\) 2 (mod. 3) ; 1985 \(\equiv\) 5 (mod. 10) ; 20 \(\equiv\) 8 (mod. 12).

L’arithmétique modulaire est enseignée en Terminale Scientifique, pour ceux qui choisissent la spécialité mathématiques.
Autant dire à des années de ce que pourrait comprendre un élève de collège…

Et pourtant… Les tables de multiplication, ces simples tables que l’on nous fait mémoriser dès notre plus jeune âge, cachent une incroyable beauté modulaire.

L’enfantine idée est la suivante : considérons la table de 3 modulo 10.

3 × 1 = 3,   donc 3 × 1 \(\equiv\) 3 (mod. 10)
3 × 2 = 6,   donc 3 × 2 \(\equiv\) 6 (mod. 10)
3 × 3 = 9,   donc 3 × 3 \(\equiv\) 9 (mod. 10)
3 × 4 = 12, donc 3 × 4 \(\equiv\) 2 (mod. 10)
3 × 5 = 15, donc 3 × 5 \(\equiv\) 5 (mod. 10)
3 × 6 = 18, donc 3 × 6 \(\equiv\) 8 (mod. 10) etc.

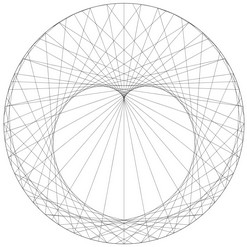
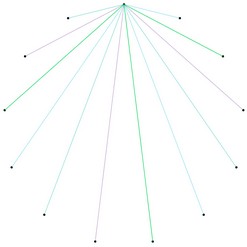
Représentons maintenant ces calculs sur un cercle. Nous y plaçons 10 points, numérotés de 0 à 9.

Puisque 3 × 1 \(\equiv\) 3 (mod. 10), nous relions le « 1 » au « 3 ».
Puisque 3 × 2 \(\equiv\) 6 (mod. 10), nous relions le « 2 » au « 6 ».
Puisque 3 × 3 \(\equiv\) 9 (mod. 10), nous relions le « 3 » au « 9 ».
Puisque 3 × 4 \(\equiv\) 2 (mod. 10), nous relions le « 4 » au « 2 ».
Etc.

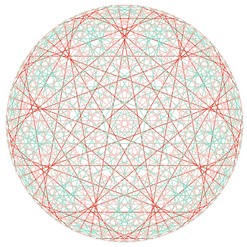
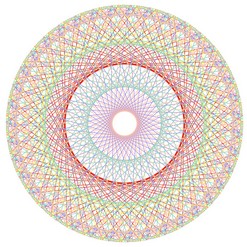
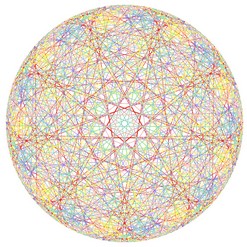
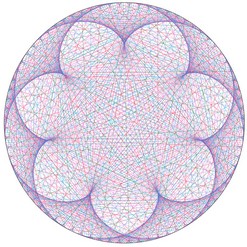
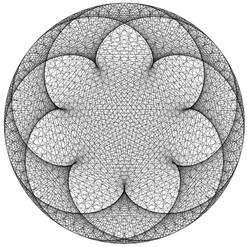
Nous obtenons alors le dessin ci-contre, qui révèle une surprenante structure symétrique.

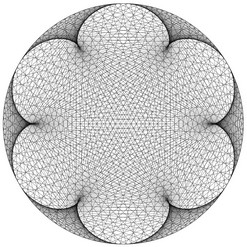
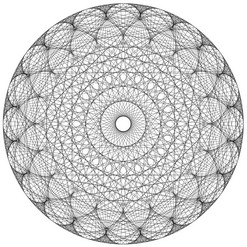
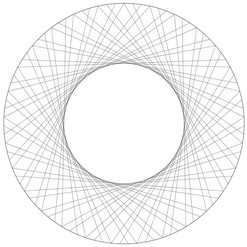
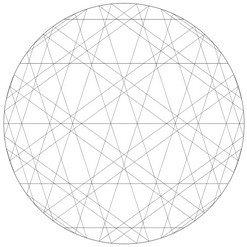
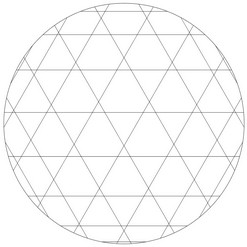
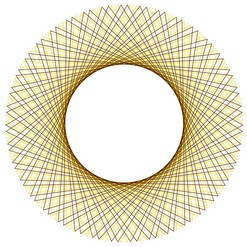
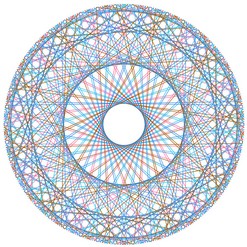
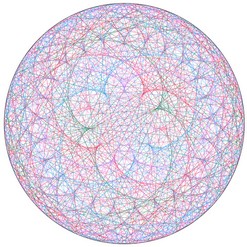
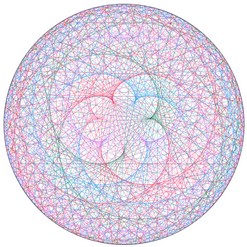
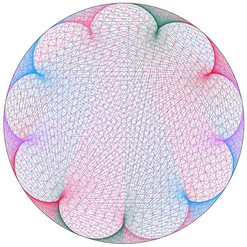
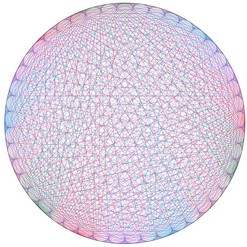
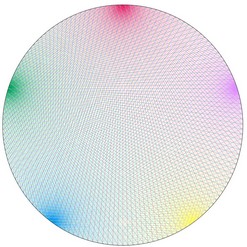
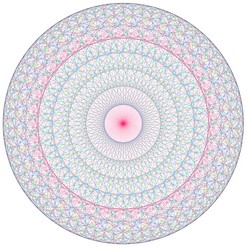
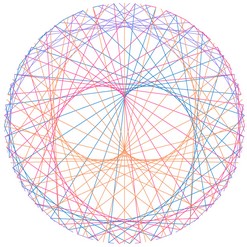
Et si nous regardions la table de 3 « de l’horloge » (table de 3 modulo 60) ? Et celle de 5 ?


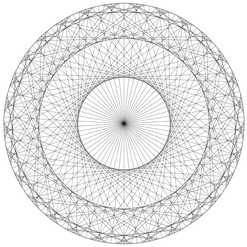
Table de 3 modulo 60	Table de 5 modulo 60

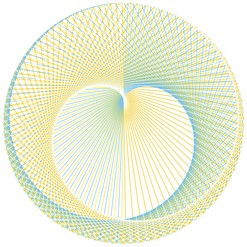
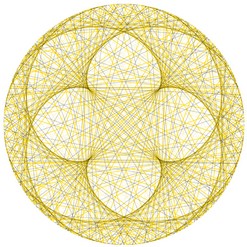
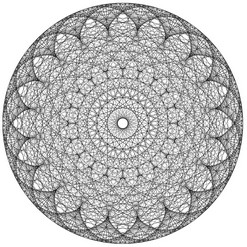
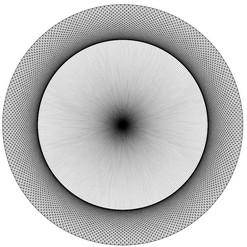
Surprenant, non ?! Et si nous nous amusions encore un peu...


Table de 7 modulo 500	Table de 21 modulo 500

Table de 30 modulo 88	Table de 30 modulo 87

Table de 47 modulo 60	Table de 30 modulo 232

Table de 16 modulo 51	Table de 77 modulo 52

Table de 242 modulo 362	Table de 767 modulo 13

Table de 781 modulo 234	Table de 791 modulo 794

Table de 792 modulo 794	Table de 1051 modulo 378

Table de 1225 modulo 493	Table de 1508 modulo 46

Table de 1648 modulo 513	Table de 1797 modulo 513

Table de 1806 modulo 773	Table de 1819 modulo 585

Table de 1834 modulo 585	Table de 1837 modulo 585

Table de 1990 modulo 585	Table de 207 modulo 691

Table de 334 modulo 691	Table de 350 modulo 691

Table de 462 modulo 691	Table de 464 modulo 691

Table de 581 modulo 691	Table de 588 modulo 691

Table de 622 modulo 691	Table de 623 modulo 691

Table de 737 modulo 691	Table de 771 modulo 691

Table de 881 modulo 740	Table de 887 modulo 740

Table de 888 modulo 740	Table de 890 modulo 740

Table de 901 modulo 740	Table de 924 modulo 740

Table de 926 modulo 740	Table de 932 modulo 740

Table de 1148 modulo 740	Table de 676 modulo 142